| Back | << | Index | >> |
Un filtre numérique IIR ( Infinite Impulse Response ) résulte de la conversion d’un filtre analogique en filtre échantillonné.
A titre d’exemple, nous considérons le filtre analogique Passe Bas suivant :
Pente : -80 db/dec ( Filtre d’ordre 4 )
Nous allons dans un premier temps concevoir un filtre analogique de Butterworth pour répondre à ce cahier des charges.
L’objectif est d’obtenir un filtre de pente (-20*N dB/dec, N ordre du filtre), en ayant 3dB d’atténuation à la fréquence de coupure.
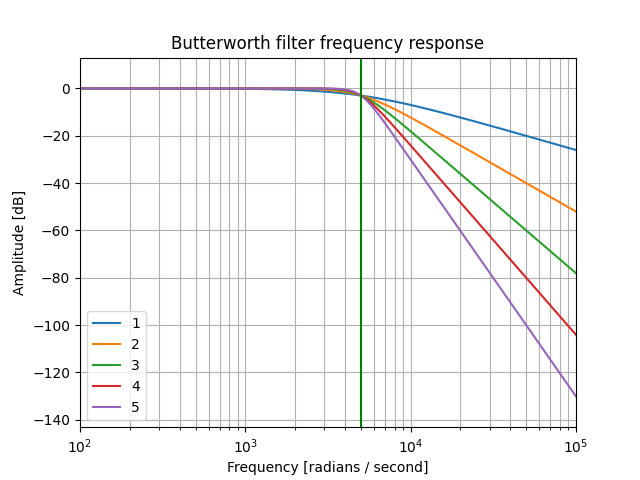
Cas N=1 :
Soit une cellule passe-bas du 1er ordre :
\(H(j\omega)=\frac{1}{1+j\frac{\omega}{\omega_c}}\)
\(\left|H(\omega)\right|=\frac{1}{\left|1+\frac{\omega}{\omega_c} \right|}\)
\(\left|H(\omega)\right|=\frac{1}{\sqrt{1+\left(\frac{\omega}{\omega_c}\right)^2}}\)
\(\left|H(\omega)\right|^2=\frac{1}{1+\left(\frac{\omega}{\omega_c}\right)^2}\)
On retrouve le cas particulier du filtre de Butterworth avec N=1.
Cas N=2 :
Soit une cellule passe-bas du 2nd ordre , avec \(\xi =\frac{\sqrt{2}}{2}\).
Ce cas particuliers permet de respecter l’atténuation de -3dB à \(f_c\)
\(H(j\omega)=\frac{1}{1+\sqrt{2}j\frac{\omega}{\omega_c}+\left(j\frac{\omega}{\omega_c} \right)^2}\)
\(\left|H(\omega)\right|= \frac{1}{\left|1+\sqrt{2}j\frac{\omega}{\omega_c}+\left(j\frac{\omega}{\omega_c} \right)^2\right|}\)
\(\left|H(\omega)\right|= \frac{1}{\left|1-\left(\frac{\omega}{\omega_c} \right)^2+\sqrt{2}j\frac{\omega}{\omega_c}\right|}\)
…
\(\left|H(\omega)\right|^2=\frac{1}{1+\left(\frac{\omega}{\omega_c}\right)^4}\)
On retrouve le cas particulier du filtre de Butterworth avec N=2.
\(s=j\frac{\omega}{\omega_c}\)
\(N\ \ \ \ Polynôme\)
\(1\ \ \ \ s+1\)
\(2\ \ \ \ s^2+1.4142s+1\)
\(3\ \ \ \ (s+1)(s^2+s+1)\)
\(4\ \ \ \ (s^2 + 0.765367s + 1)(s^2 + 1.847759s + 1)\)
\(5\ \ \ \ (s+1)(s^2+0.618s+1)(s^2+1.618s+1)\)
\(6\ \ \ \ (s^2 + 0.5176387s + 1)(s^2 + 1.414214 + 1)(s^2 +1.931852s + 1)\)
etc…
Nous allons un filtre numérique IIR, basé sur un filtre analogique de Butterworth, avec les caractéristiques suivantes :
\( H(s)=\frac{Y(s)}{X(s)}=\frac{1}{s^2+\frac{1}{Q}.0.765367.s+1}.\frac{1}{s^2+\frac{1}{Q}.1.847759.s+1} \)
\( H(f)=\frac{Y(s)}{X(s)}=\frac{1}{\left (j\frac{f}{f_c}\right )^2+j\frac{1}{Q}.0.765367.\frac{f}{f_c}+1}. \frac{1}{\left (j\frac{f}{f_c}\right )^2+j\frac{1}{Q}.1.847759.\frac{f}{f_c}+1} \)
Nous avons évoqué dans la partie echantillonage
une méthode d’intégration basée sur la méthode des trapèzes : la transformation bilinéaire.
En pratique il suffit de réaliser la substitution suivante afin de convertir un filtre analogique
en un filtre numérique :
\( s \rightarrow \frac{2}{T_e}\frac{1-z^{-1}}{1+z^{-1}} \)
Conséquence :
\( \omega_a = \frac{2}{T_e}\tan\left( \omega_c\frac{T_e}{2}\right) \)
1- A partir de l’ordre du filtre indiqué par le cahier des charges, on en déduit les polynômes de Butterworth correspondants.
2- Comme la transformée bilinéaire induit une distorsion non linéaire de l’axe fréquentiel, on corrige
la fréquence de coupure souhaitée ( prewarping)
\( \omega_a = \frac{2}{T_e}\tan\left( \omega_c\frac{T_e}{2}\right) \)
3- On applique la transformée bilinéaire
\( s \rightarrow \frac{2}{T_e}\frac{1-z^{-1}}{1+z^{-1}} \)
Filtre IIR d’Ordre 2
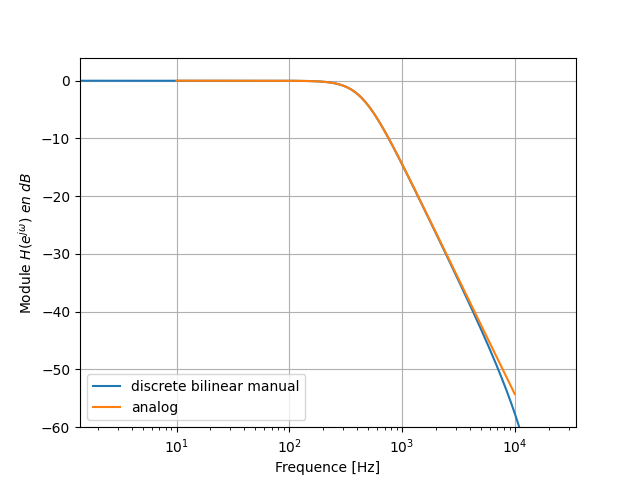
Filtre IIR d’Ordre 4
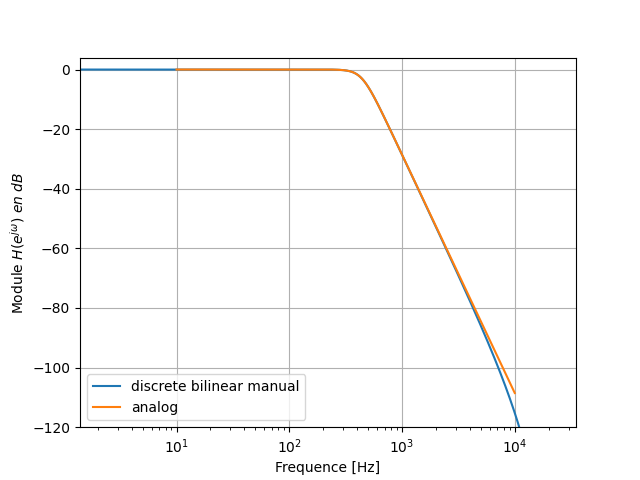
| Back | << | Index | >> |