| Back | << | Index | >> |
Fourier permet une analyse spectrale d’un système, comme la conception d’un filtre par exemple pour étudier l’attitude du système vis à vis des sinusoïdes à diverses fréquences.
Dans une application d’automatique où les signaux sont plutôt des échelons ou des rampes, la transformée de Fourier diverge.
Nous avons tenté malgré tout d’utiliser Fourier avec un échelon ; force est de constater que le calcul est compliqué.
Dans fourier, nous considérons des signaux sinusoïdaux.
Or, lorsqu’on résout des équations différentielles, apparaissent des exponentielles pour traduire l’amortissement ( ou l’amplification ).
Dès lors Laplace consiste à ajouter une composante exponentielle à la transformée de fourier :
\( Y(\sigma, f) = \int_{-\infty}^{+\infty}y(t)e^{-\sigma t}e^{-j2\pi f t } dt \)
\( Y(\sigma, \omega) = \int_{-\infty}^{+\infty}y(t)e^{(-\sigma-j\omega) t } dt \)
\( Y(s) = \int_{-\infty}^{+\infty}y(t)e^{-st} dt \)
\( \mathcal{L}[y(t)]=Y(s)=\int_{0}^{+\infty}y(t)e^{-st}dt \)
REM: Défini pour une fonction y(t) causale (t>0)
Transformée de Laplace inverse
Ce n’est pas simple vu qu’il faut intégrer un complexe avec 2 composantes variables :
\( \mathcal{L}^{-1}[Y(s)]=y(t)=\frac{1}{2\pi j} \int_{-\infty}^{+\infty}Y(s)e^{st}ds \)
où le chemin d’intégration ( parcours de s) peut être choisi quelconque dans le plan complexe à condition de rester dans le domaine de convergence de Y(s).
En pratique on décompose Y(s) en somme de fractions rationnelles simples, puis on utilise des tables .
Comme pour Fourier, nous allons “sonder” notre signal à l’aide de sinusoides, cette fois modulées en amplitude par l’exponentielle.
Autrement dit, à chaque point complexe \( s=\sigma + j.\omega \), j’associe un point complexe Y(s), résultat de l’intégrale \( Y(s) = \int_{-\infty}^{+\infty}y(t)e^{-st} dt \).
Faisons l’analyse d’un système de type intégrateur ( f(t) = 1 pour t>0 ) :
REM : les vecteurs sont sommés par l’intégrale pour trouver un point F(s).
A partie de ces calculs, je peux déterminer 4 points complexes F(s) tels que :
\( (\sigma , \omega) –> F(\sigma , \omega) \)
Et les placer dans le plan de F(s).
S’agissant de nombres complexes, on représente d’une part l’amplitude et d’autre part la phase.
| Un zoom ci-dessous pour le placement du point | F(s) | tel que s=0.5+0.5.j : |
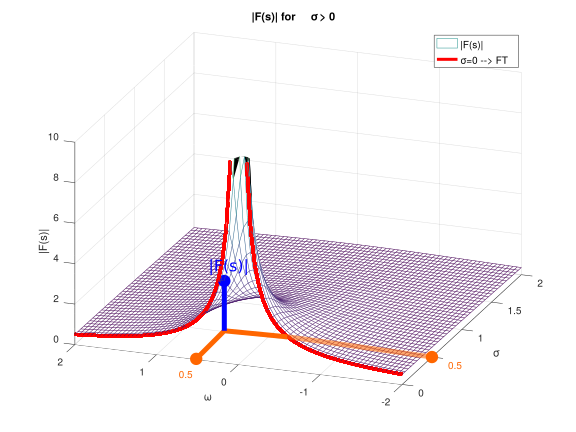
REMARQUE : quand \( \sigma = 0 \) : \( Y(0, \omega) = \int_{-\infty}^{+\infty}y(t)e^{j\omega t } dt \)
On retrouve la TRANSFORMEE DE FOURIER ( courbe rouge sur la figure ci-dessus).
La transformée de fourier est donc un cas particulier de Laplace.
Laplace généralise Fourier.
Si ce système intégrateur est excité par un signal de fréquence et d’amortissement nul, par exemple x(t)=step(t), alors la transformée est infinie.
On dit que le cas s=0 constitue un pôle du système.
\( step(t) \overset{\mathcal{L}}{\rightarrow} \frac{1}{s} \)
\( \delta(t) \overset{\mathcal{L}}{\rightarrow} 1 \)
\( e^{-a.t}step(t) \overset{\mathcal{L}}{\rightarrow} \frac{1}{s+a} \)
\( Y(s) = \int_{0}^{+\infty}y(t)e^{-st} dt \)
prenons par exemple \( y(t) = e^{-at} \)
\( Y(s) = \int_{0}^{+\infty}e^{-at}e^{-st} dt \)
\( Y(s) = \int_{0}^{+\infty}e^{-at}e^{-\sigma t}e^{-j\omega t} dt \)
\( Y(s) = \int_{0}^{+\infty}e^{-(a+\sigma ) t}e^{-j\omega t} dt \)
Cette intergrale converge si : \( a+\sigma >0 \) –> \( \sigma >-a \)
\( Y(s) = \frac{1}{s+a} \)
-a constitue un pôle de Y ( valeur pour laquelle \( Y(s) = \infty \)
La région de convergence de Y(s) correspond aux points s tels que \( \Re e(s)>-a \)
Cela peut être représenté par une vue de dessus simplifiée des schémas 3D précédents :
\( \mathcal{L} \left [\frac{dy(t)}{dt} \right ]=\int_{0}^{+\infty}\frac{dy(t)}{dt}e^{-st}dt \)
Intégration par parties :
\( \mathcal{L} \left [ \frac{dy(t)}{dt} \right ]= \left [ y(t)e^{-st} \right ]-\int_{0}^{+\infty}(-s)y(t)e^{-st}dt \)
\( \mathcal{L} \left [\frac{dy(t)}{dt} \right ]=sY(s)-y(0) \)
\( \int{y(t).dt}=\frac{Y(s)}{s} \)
\( \lim_{s \to \infty}sY(s)=y(0-)+\lim_{s \to \infty}\left ( \int_{0-}^{+\infty}\frac{dy(t)}{dt}e^{-st}dt \right ) = y(0-)+[y(0+)-y(0-)] \)
\( \lim_{s \to \infty}sY(s)=y(0+) \)
\( \lim_{s \to 0}sY(s)=y(0-)+\lim_{s \to 0}\left ( \int_{0-}^{+\infty}\frac{dy(t)}{dt}e^{-st}dt \right ) = y(0-)+[y(+\infty)-y(0-)] \)
\( \lim_{s \to 0}sY(s)=y(+\infty) \)
\( \mathcal{L}[y(t)]= \mathcal{L}[(h\otimes x)(t)] \)
\( Y(s)=\mathcal{L}[\int_{-\infty}^{+\infty}h(t-\theta).x(\theta)d\theta] \)
\( Y(s)=\int_{0}^{+\infty}(\int_{0}^{+\infty}h(t-\theta).x(\theta)d\theta)e^{-st}dt \)
Changement de variable
\( v=t-\theta \)
\( Y(s)=\int_{0}^{+\infty}\int_{0}^{+\infty}h(v)x(\theta) e^{-s(v+\theta)}d\theta dv \)
\( Y(s)= \int_{0}^{+\infty}h(v)e^{-sv}dv+\int_{0}^{+\infty}x(\theta)e^{-s\theta}d\theta \)
\( Y(s)=\mathcal{L}[h].\mathcal{L}[x] \)
\( Y(s)=H(s).X(s) \)
–> Le produit de Convolution en temporel devient un simple produit dans le domaine de Laplace .
à partir de l’équation différentielle :
\( \tau \frac{dy(t)}{dt}+y(t)=G.x(t) \)
\( \mathcal{L} \left[ \tau \frac{dy(t)}{dt}+y(t) \right]=\mathcal{L} \left[ G.x(t) \right] \)
\( \mathcal{L} \left[ \tau \frac{dy(t)}{dt} \right] +\mathcal{L} \left[y(t) \right]=G.\mathcal{L} \left[ x(t) \right] \)
\( \tau.sY(s)+Y(s) = G.X(s) \)
\( Y(s)=\frac{G}{1+\tau .s }X(s) \)
\( X(s)=\frac{1}{s} \)
\( H(s)=\frac{G}{1+\tau .s} \)
Tracé de laplace de H(s) pour G=10 et \( \tau=1 \)
REMARQUE : en rouge la Transformée de Fourier de la fonction de transfert ( ou réponse impulsionnelle) = tracé du Bode.
\( Y(s)=H(s).X(s)= \frac{1}{s}.\frac{G}{1+\tau .s} \)
\( Y(s)= \frac{\alpha}{s}+\frac{\beta}{1+\tau .s} \)
par identification :
\( Y(s)= \frac{G}{s}-\frac{\tau.G}{1+\tau .s} \)
\( Y(s)= \frac{G}{s}-\frac{G}{\frac{1}{\tau}+s} \)
Rappelons nous la résolution de l’équation différentielle, on retrouve :
Transformée inverse de Laplace (utilisation des tables) :
\( y(t)=step(t).G(1-e^{-\frac{t}{\tau}}) \)
En posant \( s=j\omega \)
\( H(s)=H(j\omega) = \frac{G}{1+\frac{j\omega}{\omega_0}} \) \( avec \ \tau=\frac{1}{\omega_0} \)
On retrouve donc la fonction de transfert d’un sytème en régime sinusoïdal.
On peut donc retrouver la fonction de transfert de laplace à partir des impédances en régime sinusoidal (cf sinus.html et bode.html )
| Back | << | Index | >> |